Graph++

Motivations

As part of our coursework in data structure & algorithms, and desktop development, we were tasked as students to develop a desktop application that implemented mutliple data structures and algorithms seen in class. In collaboration with my classmates Simon Plumey and Damien Tschan, we focused our work on implementing graph structures, and some of the standard graph algorithms one might use to process and study graphs, in an Adobe-style desktop app. In order to combine speed, good control over data structures, and the possibility to build a complex desktop application, we took the decision to work with C++ and the Qt framework.

Concept

The project is built around three main components:

1. The library
2. The test suite
3. The desktop app

The library contains the core data structures and algorithms, implemented in pure C++ with no dependencies. This library can be used as a stand-alone component in other projects, and allows building flexible graph structures.

The test suite is a battery of tests built to assess the correctness of the library, and systematically perform different operations on the generated graphs.

The desktop app, built using the core library, allows a user to easily build and edit graphs in a standard Adobe-style desktop application. The app also allows to perform the algorithms implemented in the library.

Architecture

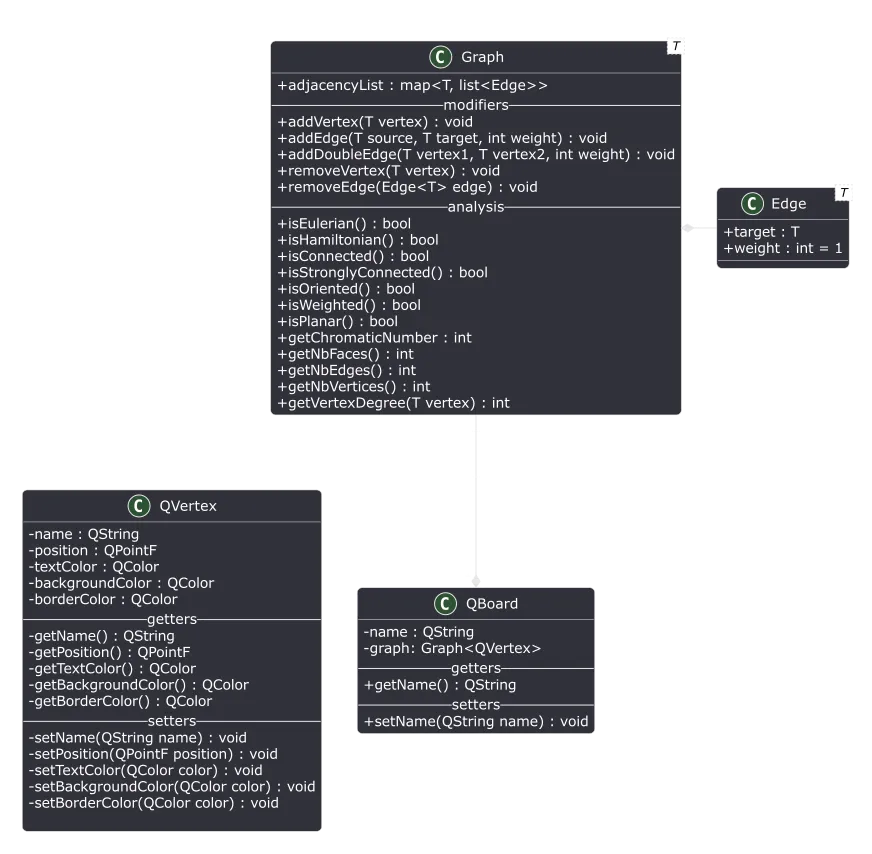
The library is built around the main class Graph<T>. As you can see, the class is templated, which allows the user to build a graph, where nodes are instances of any class T. This is particularly useful, as graphs might be used to represent locations on a map, states of a system, people, or many other concepts. This architecture allows the library to be seamlessly used with any data structure the user defines.

In our case, this is used in the GUI application, by building a data structure that will represent an actual point in the drawing space of the application, with attributes such as position, color, etc.

As a stand-alone component, the library has an intuitive API that can be easily used to quickly run standard algorithms.

#include <graph.h>

    ///.......
    // Create some vertices
    int vertices[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};

    // Create a graph for those vertices
    Graph<int>* graph = new Graph<int>();

    // Add the vertices to the graph
    for(int i : vertices){
        graph->addVertex(&i);
    }

    // Add some edges to the graph (Circular graph)
    for(int i : vertices){
        int nextIndex = i + 1;
        if(nextIndex >= nbVertices){
            nextIndex = 0;
        }
        graph->addDoubleEdge(&vertices[i], &vertices[nextIndex]);
    }

    // Basic properties
    std::cout << graph->getNbVertices() << std::endl;
    std::cout << graph->getNbEdges() << std::endl;
    std::cout << graph->isOriented() << std::endl;
    std::cout << graph->isWeighted() << std::endl;

    // Algorithms
    Graph<int>* hamiltionianPath = graph->getHamiltonianPath();
    Graph<int>* shortestPathGraph = graph->getMinimumDistanceGraph(&vertices[3]);
    Graph<int>* minimumSpanningTree = graph->getMinimumSpanningTree();

Algorithms

In the library, multiple algorithms are implemented. These algorithms allow the computation of graph properties, such as the chromatic number, or whether the graph is eulerian. Additionnaly, some algorithms allow to compute subsets of the graph that possess specific properties, such as the minimum spanning tree or the minimum distance graph. These algorithms leverage the inner data structures of the graph: minimum priority queues and adjacency lists.

Some of the algorithms implemented include:

• Prim’s algorithm as Graph<T>::getMinimumSpanningTree()
• Dijkstra’s algorithm as Graph<T>::getMinimumDistanceGraph(T *startingVertex)
• The greedy graph coloring algorithm as Graph<T>::getChromaticNumber()
• Euler’s theorem for eulerian paths/circuits as Graph<T>::isEulerian()